13 Algoritmos cuánticos

Sección en construcción.

En esta sección presentaremos tres algoritmos cuánticos que muestran las ventajas de un sistema de computación cuántico con respecto a uno clásico. En concreto, analizaremos el algoritmo de Deutsch-Jotzsa, el algoritmo de búsqueda de Grover, y el algoritmo de factorización de Shor.

13.1 Algoritmo de Deutsch-Jotzsa

Consideremos una función booleana $f$ con $n$ bits de entrada y $1$ bit de salida: $$\begin{align*} f:\{0,1\}^n\to\{0,1\} \end{align*}$$ El algoritmo de Deutsch-Jotzsa permite determinar ciertas propiedades de una función booleana $f$ sin necesidad de evaluar la función para todas las posibles entradas. En particular, es capaz de determinar si una función booleana $f$ es constante o balanceada.

Definición 13.1 La función $f$ es constante si siempre devuelve el mismo valor (bien $0$ o $1$) para todas las entradas. La función $f$ es balanceada si devuelve $0$ para exactamente la mitad de las entradas y $1$ para la otra mitad.

Ejemplo 13.1 Consideremos las siguintes funciones booleanas $f:\{0,1\}^2\to\{0,1\}$:

• $f(a,b) = a \oplus b$ (función XOR $\equiv$ OR exclusivo). Esta función devuelve $$\begin{align*} f(0,0) = 0,\quad f(0,1) = 1,\quad f(1,0) = 1,\quad f(1,1) = 0, \end{align*}$$ y por tanto se trata de una función balanceada (mismo número de $0$ y de $1$ a su salida).

• $f(a,b) = 0$ (función ‘0’). Esta función devuelve $$\begin{align*} f(0,0) = 0,\quad f(0,1) = 0,\quad f(1,0) = 0,\quad f(1,1) = 0, \end{align*}$$ y por tanto se trata de una función constante (siempre devuelve $0$).

• $f(a,b) = a \wedge b$ (función AND). Esta función devuelve $$\begin{align*} f(0,0) = 0,\quad f(0,1) = 0,\quad f(1,0) = 0,\quad f(1,1) = 1, \end{align*}$$ y por tanto esta función no es ni constante ni balanceada.

Planteamiento del problema

Tenemos acceso a una caja negra que permite evaluar una función $f$, de la que sabemos que es bien constante o balanceada (pero sólo una de estas dos alternativas). Nos piden determinar de forma unívoca qué tipo de función es con el mínimo número de llamadas o evaluaciones de la función.

Nuestra intuición nos indica que, dado que no conocemos ninguna información sobre la función $f$ (excepto que es bien constante o bien balanceada), solo podemos probar algunas de las $2^n$ posibles entradas y observar su salida correspondiente. Si en este proceso observamos dos salidas diferentes sabemos con seguridad que la función no es constante, y por tanto debe ser balanceada.

Sin embargo, en el peor caso, podemos obtener $2^n / 2$ salidas iguales y todavía no podríamos descartar que la función sea constante o balanceada (dado que las otras $2^n / 2$ salidas podrían ser iguales o diferentes a las primeras). Por tanto, concluimos que, en el peor caso, necesitaremos $2^n / 2 + 1$ llamadas a la función para resolver este problema de forma unívoca.

Ejemplo 13.2 Consideremos una función booleana $f:\{0,1\}^2\to\{0,1\}$ desconocida, de la que sabemos que es o constante o balanceada. Se realizan dos llamadas a la función y se obtienen los resultados

1. $f(0,0) = 0$,

2. $f(1,1) = 0$.

Todavía no podemos asegurar si la función es constante o balanceada. De hecho, estos resultados son compatibles con las funciones $f(a,b) = a \oplus b$ y $f(a,b) = 0$ del ejemplo anterior. Así, es necesario realizar una nueva llamada a la función:

3. $f(0,1) = 1$

Obtenemos $f(0,1) \neq f(0,0)$ y por tanto concluimos que es balanceada: $f(a,b) = a \oplus b$.

Para resolver el problema planteado hemos requerido $3$ llamadas a la función.

Así, en el peor caso, no parece que sea posible resolver este problema con menos de $2^n / 2 + 1$ llamadas a la función $f$. Aunque esto es cierto para sistemas de computación clásica, veremos que utilizando las propiedades de la mecánica cuántica es posible determinar si la función es constante o balanceada con un único uso de $f$, o de forma más precisa, con un único uso de su operador cuántico asociado.

Algoritmo cuántico

Por sencillez, consideremos en primer lugar una función booleana con un único bit de entrada, $$\begin{align*} f:\{0,1\} \to\{0,1\}. \end{align*}$$ Para esta función, solo existen dos posibilidades: si $f(0)=f(1)$, la función es constante, mientras que si $f(0) \neq f(1)$ la función es balanceada. Así, para una función de entrada binaria no se puede dar el caso de que no sea ni constante ni balanceada. En un sistema de computación clásico, es necesario realizar dos llamadas a la función $f$ para comprobar si es constante o balanceada. Con una implementación cuántica, en cambio, es posible determinar esta propiedad con un único uso del operador cuántico $U_f$ asociado.

Oráculo

Este operador $U_f$ se denomina oráculo de la función $f$ y tiene la estructura vista en la sección anterior para la implementación cuántica de funciones booleanas:

donde las salidas deben cumplir $\ket{x}=\ket{a}$ e $\ket{y} = \ket{b\oplus f(a)}$.

Inicialización

Para entender el funcionamiento del algoritmo de Deutsch-Jotzsa, vamos a estudiar como se comporta el oráculo $U_f$ si introducimos en la entrada auxiliar $\ket{b}$ el cúbit $H\ket{1} = \tfrac{1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr) = \ket{-}$:

El cúbit de salida superior está dado por $\ket{x}=\ket{a}$. Por otra parte, dado que $\ket{b} = \tfrac{1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr)$, utilizando la propiedad del paralelismo cuántico,obtenemos que el cúbit de salida inferior queda $$\begin{align*} \ket{y} &= \tfrac{1}{\sqrt{2}} \bigl(\ket{0 \oplus f(a)}-\ket{1 \oplus f(a)} \bigr)\\ &= \begin{cases} \tfrac{1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr), & \text{si } f(a)=0,\\ \tfrac{1}{\sqrt{2}} \bigl(\ket{1}-\ket{0} \bigr), & \text{si } f(a)=1. \end{cases} \end{align*}$$ Usando que $\ket{-} = \tfrac{1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr)$, este estado se puede modelar de forma compacta como $$\begin{align*} \ket{y} &= (-1)^{f(a)} \ket{-}, \end{align*}$$ por lo que concluimos que cuando $f(a)=1$, se produce un cambio de signo en el cúbit de salida $\ket{y}$. Si consideramos el estado conjunto $\ket{x} \otimes\ket{y}$ a la salida del circuito, éste queda $$\begin{align*} \ket{x} \otimes \ket{y} &= (-1)^{f(a)} \bigl(\ket{a} \otimes \ket{-} \bigr). \end{align*}$$

Paralelismo cuántico

En el análisis anterior hemos determinado la salida del circuito cuántico para una entrada $\ket{a} =\ket{0}$ o $\ket{a} =\ket{1}$. En particular, evaluando la expresión anterior para $a =0,1$ obtenemos $$\begin{align} \ket{x} \otimes \ket{y} = \begin{cases} (-1)^{f(0)} \bigl(\ket{0} \otimes \ket{-} \bigr) = (-1)^{f(0)} \ket{0,-},\ &\ket{a} =\ket{0},\\ (-1)^{f(1)} \bigl(\ket{1} \otimes \ket{-} \bigr) = (-1)^{f(1)} \ket{1,-},\ &\ket{a} =\ket{1}. \end{cases} \tag{$\star$} \end{align}$$

Vamos ahora a utilizar la propiedad del paralelismo cuántico para procesar estas dos entradas al mismo tiempo. Para ello, en la entrada principal del oráculo $U_f$ aplicamos una superposición uniforme $$\ket{a} = H\ket{0} = \tfrac{1}{\sqrt{2}} \bigl(\ket{0}+\ket{1} \bigr)$$:

Según el principio del paralelismo cuántico, para una superposición de entradas, la salida se corresponde a la superposición de las salidas correspondientes. Entonces, utilizando ($\star$), obtenemos $$\begin{align*} \ket{x} \otimes \ket{y} &= \tfrac{1}{\sqrt{2}} \Bigl((-1)^{f(0)} \ket{0, -}+(-1)^{f(1)} \ket{1, -} \Bigr). \end{align*}$$

En los siguientes pasos vamos a descartar la línea de cúbits auxiliar, que se encuentra en el estado $\ket{-}$, común para ambos elementos de la misma. Así obtenemos $$\begin{align*} \ket{x} &= \tfrac{1}{\sqrt{2}} \Bigl((-1)^{f(0)} \ket{0}+(-1)^{f(1)} \ket{1} \Bigr). \end{align*}$$ Vamos a agrupar por una parte los casos $f(0)=f(1)=0$ y $f(0)=f(1)=1$, dónde los dos términos de la expresión presentan el mismo signo, bien positivo o negativo; y por otra, los casos $f(0)=0, f(1)=1$ y $f(0)=1, f(1)=0$, dónde los dos términos presentan diferentes signos. Así, la expresión anterior se puede reescribir de forma compacta como $$\begin{align*} \ket{x} &= \begin{cases} \tfrac{\pm 1}{\sqrt{2}} \bigl(\ket{0}+\ket{1} \bigr) = \pm\ket{+}, & \text{si } f(0)=f(1),\\ \tfrac{\pm 1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr) = \pm\ket{-}, & \text{si } f(0)\neq f(1). \end{cases} \end{align*}$$

Medida y resultado

Se puede comprobar que los dos casos que aparecen en esta expresión son dos estados cuánticos puros ortogonales entre sí, y se podrían distinguir sin errores mediante un proceso de medida en la base $\bigl\{\ket{+},\ket{-}\bigr\}$. Sin embargo, no es posible implementar una medida directamente en la base $\bigl\{\ket{+},\ket{-}\bigr\}$ en un ordenador cuántico, ya que este último trabaja siempre en la base computacional.

Sabemos que la puerta de Hadamard $H$ transforma la base $\bigl\{\ket{0},\ket{1}\bigr\}$ en la base $\bigl\{\ket{+},\ket{-}\bigr\}$, y viceversa. Así, si definimos un estado $\ket{z} = H\ket{x}$, tenemos que $$\begin{align*} \ket{z} = H \ket{x} &= \begin{cases} \pm \ket{0}, & \text{si } f(0)=f(1),\\ \pm \ket{1}, & \text{si } f(0)\neq f(1). \end{cases} \end{align*}$$ Si aplicamos una medida sobre el estado $\ket{z}$ con respecto a la base computacional $\bigl\{\ket{0},\ket{1}\bigr\}$, obtendremos por tanto un resultado determinista $$\begin{align*} z = \begin{cases} 0, & \text{si } f(0)=f(1),\\ 1, & \text{si } f(0)\neq f(1). \end{cases} \end{align*}$$ que va a depender de si la función es constante $f(0)=f(1)$, o balanceada $f(0)\neq f(1)$.

Algoritmo de Deutsch

El proceso descrito anteriormente fue propuesto inicialmente por David Deutsch en 1985, por lo que se conoce habitualmente como algoritmo de Deutsch (Deutsch 1985). La siguiente figura muestra el diagrama de bloques completo de este algoritmo:

Para determinar si la función $f$ es constante o balanceada, ejecutamos el algoritmo en un ordenador cuántico y comprobamos el resultado:

• Si $z=0$, entonces la función $f$ es constante.
• Si $z=1$, entonces la función $f$ es balanceada.

Este algoritmo permite determinar si la función $f: \{0,1\} \to\{0,1\}$ es constante o balanceada mediante un único uso del oráculo $U_f$. Por otra parte, el mejor algoritmo clásico para hacer esto requería dos llamadas a la función $f$.

Ejercicio 13.1 Considere la función booleana de entrada binaria $f(a)=\text{NOT}(a)$. ¿Cual debería ser la salida del algoritmo de Deutsch para esta función? El oráculo cuántico $U_f$ asociado a $f$ es Implemente el algoritmo de Deutsch en IBM Quantum y ejecútelo. ¿Da el resultado esperado?

Repita el proceso para los siguientes oráculos ¿Qué funciones booleanas representa cada uno de estos oráculos? ¿Funciona el algoritmo?

Algoritmo de Deutsch-Jotzsa

La idea del algoritmo de Deutsch se extendió también para considerar funciones booleanas con $n$ entradas en un trabajo realizado por el propio Deutsch en colaboración de Richard Jozsa (Deutsch and Jozsa 1992). Esta extensión, conocida como algoritmo de Deutsch-Jotzsa, permite determinar si una función $$f:\{0,1\}^n\to\{0,1\}$$ es constante o balanceada mediante un único uso del operador $U_f$.

La siguiente figura muestra el diagrama de bloques del algoritmo de Deutsch-Jotzsa:

Mientras que en el caso de $n=1$ la ventaja del algoritmo cuántico es marginal (pasamos de dos usos de la función $f$ a un único uso del oráculo $U_f$), para el caso de funciones con $n$ entradas, el algoritmo cuántico presenta una ventaja exponencial sobre el clásico: El algoritmo clásico (en el peor caso) requiere $2^n/2+1 = 2^{n-1}+1$ llamadas a la función $f$, mientras que el algoritmo de Deutsch-Jozsa ofrece una solución determinista con un único uso del oráculo $U_f$:

• Si $\boldsymbol{z}=0$, entonces la función $f$ es constante.
• Si $\boldsymbol{z}\neq 0$, entonces la función $f$ es balanceada.

A pesar de que el problema de distinguir si una función es constante o balanceada carece de utilidad práctica, este algoritmo fue la primera demostración de que los ordenadores cuánticos permiten resolver ciertos problemas de una forma (exponencialmente) más rápida que el mejor ordenador clásico. Así, este resultado impulsaría el desarrollo y búsqueda de otros algoritmos que acabarían teniendo grandes implicaciones, como veremos a continuación.

13.2 Algoritmo de búsqueda de Grover

Consideremos ahora una función booleana $f:\{0,1\}^n \to \{0,1\}$ tal que $$\begin{align*} f(\boldsymbol{x}) &= \begin{cases} 1, & \text{si } \boldsymbol{x} = \boldsymbol{x}^{\star},\\ 0, & \text{si } \boldsymbol{x} \neq \boldsymbol{x}^{\star}. \end{cases} \end{align*}$$ Es decir, la función se activa para una entrada $\boldsymbol{x}^{\star}$ y permanece inactiva para las demás entradas.

Planteamiento del problema

Para una función $f:\{0,1\}^n \to \{0,1\}$ desconocida tal que $f(\boldsymbol{x})=1$ para una (y solo una) entrada $\boldsymbol{x} = \boldsymbol{x}^{\star}$, deseamos encontrar el valor que activa la función $\boldsymbol{x}^{\star}$.

Se debe tener en cuenta que este problema se corresponde con una búsqueda de un único elemento en un espacio con $2^n$ posibilidades. Por ejemplo, para $n=16$ tendríamos que encontrar la entrada que activa la función entre más de 65 mil posibilidades. Así, podemos pensar en este problema como “encontrar una aguja en un pajar”.

El mejor algoritmo clásico para resolver este problema tiene complejidad $\mathcal{O}(N)$ con $N=2^n$, ya que requiere (en el peor caso) $N-1$ llamadas a la función para encontrar la entrada que la activa. En cambio, un algoritmo cuántico desarrollado por Lov Grover en 1996 puede resolver este problema con solo $\mathcal{O}(\sqrt{N})$ usos del oráculo $U_f$ asociado a la función (Grover 1996).

A diferencia del algoritmo de Deutsch-Jozsa, esta formulación permite modelar diversos problemas de índole práctica, como pueden ser:

• La búsqueda dentro de una lista desordenada de $N = 2^n$ elementos. Por ejemplo, en una base de datos podríamos buscar en qué registro se encuentra un determinado dato, de ahí su denominación habitual como algoritmo de búsqueda de Grover.

• Un ataque por fuerza bruta a un sistema criptográfico con $N = 2^n$ posibles entradas (claves) en el cual una única posibilidad es la correcta. Si disponemos de una función $f$ que nos indique si la clave funciona (por ejemplo,comprobando que el archivo desencriptado cumple ciertas propiedades), entonces podemos modelar el problema de búsqueda de la clave de esta forma.

Este resultado presenta unas enorme implicaciones, ya que permite, por ejemplo, acelerar un ataque de fuerza bruta pasando de requerir probar $N=2^n$ claves, a tan solo $\sqrt{N} = 2^{n/2}$ evaluaciones de la función. Así, si consideramos un sistema criptográfico con una clave de longitud $n$ bits, estaríamos reduciendo su longitud efectiva de la clave a la mitad.

Operador de difusión de Grover

La pieza clave del algoritmo de Grover es el denominado operador de difusión de Grover $G$.

La transformación unitaria $G$ se define como $$\begin{align*} G \,=\, H^{\otimes n}\Bigl(2 \ket{0^n}\bra{0^n} - I_n\Bigr) H^{\otimes n} \,=\, 2 \ket{\psi}\bra{\psi} - I_n, \end{align*}$$ donde $\ket{\psi}$ es una superposición uniforme e $I_n$ es el operador identidad.

Para ilustrar el efecto del operador de difusión $G$ consideremos el estado puro $$\begin{align*} \ket{a} = \sum\nolimits_{i} a_i \ket{i} \end{align*}$$ donde $\ket{i}$ denota el estado cuántico de la base computacional asociado a la descomposición binaria de $i=0,1, \ldots,N-1$, y donde $a_i$ denota su correspondiente amplitud de probabilidad.

Ejemplo 13.3 Para $n=3$, $N=2^n=8$, la superposición uniforme está dada por $$\begin{align*} \ket{\boldsymbol{a}} & = \frac{1}{\sqrt{8}} \bigl(\ket{000}+\ket{001}+\ket{010}+\ket{011}+\ket{100}+\ket{101}+\ket{110}+\ket{111} \bigr), \end{align*}$$ con índices asociados $i=0,1,2,\ldots, 7$.

Los términos de amplitud de probabilidad para $i=0,1,2,\ldots,7$ están dados por $a_i = \frac{1}{\sqrt{8}}$:

Si aplicamos el operador de difusión $G$ a un estado $$\begin{align*} \ket{a} = \sum_{i} a_i \ket{i} \end{align*}$$ con valor de amplitud de probabilidad medio $\bar a = \frac{1}{N} \sum_i a_i$, a su salida obtendremos $$\begin{align*} \ket{b} = G \ket{a} = \sum_{i} (2 \bar a - a_i) \ket{i}. \end{align*}$$ El operador $G$ transforma así las amplitudes de probabilidad de la superposición a su entrada $a_i$ en amplitudes de probabilidad $b_i = 2 \bar a - a_i$ a su salida. El siguiente ejemplo muestra como esta transformación es capaz de convertir diferencias de fase en diferencias de amplitud a su salida.

Ejemplo 13.4 Vamos a aplicar el operador de difusión $G$ a un estado $\ket{a} = \sum_{i} a_i \ket{i}$, y observar su efecto en la salida $\ket{b} = \sum_{i} b_i \ket{i} = G \ket{a}$.

Para $n=3$, $N=2^n=8$, consideremos una superposición con amplitudes de probabilidad: $$\begin{align*} a_i = \begin{cases} \frac{1}{\sqrt{8}}, & i \neq 3,\\ -\frac{1}{\sqrt{8}}, & i = 3. \end{cases} \end{align*}$$ Podemos ver que todas las amplitudes de probabilidad tienen módulo $|a_i|^2 =\frac{1}{8}$, aunque la amplitud correspondiente al estado $\ket{011}$ ($i=3$), presenta una fase diferente a las demás. Si aplicamos el operador de difusión $G$, a su salida obtenemos las amplitudes de probabilidad $$\begin{align*} b_i = \begin{cases} \frac{1}{2\sqrt{8}}, & i \neq 3,\\ \frac{5}{2\sqrt{8}}, & i = 3. \end{cases} \end{align*}$$ Así, el operador de difusión $G$ transforma las diferencias de fase en la superposición de entrada en diferencias de amplitud en la superposición de salida:

Ejercicio 13.2 Para $n=2$, $N=4$, Obtenga las amplitudes de probabilidad de salida $b_i$ del estado $\ket{b} = \sum_{i} b_i \ket{i} = G \ket{a}$ para los siguientes estados de entrada $\ket{a}$:

1. Superposición uniforme: $$\begin{align*} \ket{\boldsymbol{a}} & = \frac{1}{2} \bigl(\ket{00}+\ket{01}+\ket{10}+\ket{11} \bigr). \end{align*}$$

2. Un elemento de la superposición con fase negativa: $$\begin{align*} \ket{\boldsymbol{a}} & = \frac{1}{2} \bigl(\ket{00}-\ket{01}+\ket{10}+\ket{11} \bigr). \end{align*}$$

3. Dos elementos de la superposición con fase negativa: $$\begin{align*} \ket{\boldsymbol{a}} & = \frac{1}{2} \bigl(\ket{00}-\ket{01}+\ket{10}-\ket{11} \bigr). \end{align*}$$

Algoritmo cuántico

Al igual que en el algoritmo de Deutsch-Jozsa necesitamos un oráculo de la función $f$ a analizar:

Inicialización

La inicialización y primeros pasos del algoritmo de Grover coinciden con los correspondientes pasos del algoritmo de Deutsch-Jozsa. Tal y cómo hemos visto en la sección anterior, si introducimos el cúbit $H\ket{1} = \tfrac{1}{\sqrt{2}} \bigl(\ket{0}-\ket{1} \bigr) = \ket{-}$ en la entrada auxiliar de $U_f$, a su salida obtenemos $$\begin{align*} U_f \ket{\boldsymbol{a}, -} = \begin{cases} -\ket{\boldsymbol{a}, -},& f(\boldsymbol{a})=1,\\ +\ket{\boldsymbol{a}, -},& f(\boldsymbol{a})=0. \end{cases} \end{align*}$$ Es decir, el estado a la salida pasa a tener una amplitud negativa para $\boldsymbol{a}=\boldsymbol{x}^{\star}$.

Paralelismo cuántico

En la entrada principal del operador cuántico introducimos una superposición uniforme como la vista en el Ejemplo 13.3: $$\begin{align*} \ket{\boldsymbol{a}} &= H^{\otimes n} \ket{0^{\otimes n}} = \frac{1}{\sqrt{N}} \sum_{i=0}^{N-1} \ket{i}. \end{align*}$$ Por la propiedad del paralelismo cuántico, aplicando esta entrada al oráculo con la inicialización considerada en el punto anterior, a su salida obtendremos una superposición de salidas: $$\begin{align*} U_f \ket{\boldsymbol{a}, -} = \frac{1}{\sqrt{N}} \sum_{i=0}^{N-1} (-1)^{f(i)} \ket{i, -}. \end{align*}$$ De esta forma, los elementos de la superposición tales que $f(i) = 0$ permanecen inalterados, mientras que los elemento de la superposición con $f(i) = 1$ pasan a tener una amplitud de probabilidad negativa.

Ejemplo 13.5 Vamos a considerar una función booleana con $n=2$ bits de entrada que se activa con $f(0,1)=1$, siendo cero en los demás casos. Si aplicamos a la entrada al oráculo la superposición uniforme $\ket{\boldsymbol{a}} = \frac{1}{2} \bigl(\ket{00}+\ket{01}+\ket{10}+\ket{11} \bigr)$ con la inicialización del punto anterior, a su salida obtenemos $$\begin{align*} U_f \ket{\boldsymbol{a}, -} & = \frac{1}{2} \bigl(\ket{00,-}-\ket{01,-}+\ket{10,-}+\ket{11,-} \bigr). \end{align*}$$ El estado $\ket{01,-}$ presenta un signo negativo debido al término $(-1)^{f(i)}$ que se activa para la entrada (y solo para la entrada) $i=01$.

Operador de difusión y medida

Así, a la salida del oráculo, hemos marcado los elementos de la superposición $\ket{i}$ tales que $f(i) = 1$ con una amplitud de probabilidad negativa. Sin embargo, todavía no es posible hacer una medida del sistema que nos permita determinar estos elementos, ya que la probabilidad de medida es proporcional al módulo cuadrado de las amplitudades, y no depende de su fase.

Aquí es donde entra en juego el operador de difusión de Grover $G$, que transforma diferencias de fase en diferencias de amplitud. Este operador amplifica la amplitud del término negativo mientras que reduce la amplitud de los demás términos, tal y cómo hemos visto en el Ejemplo 13.4.

En el algoritmo de Grover, el oráculo y el operador de difusión se deben aplicar $\mathcal{O}(\sqrt{N})$ veces para maximizar el módulo del elemento deseado, mientras que se minimiza el módulo de la amplitud de los demás elementos.

Una vez se ha realizado este proceso se aplica un proceso de medida en la base computacional, que resulta en la solución correcta $\boldsymbol{x}^{\star}$ de forma determinista, o con alta probabilidad.

Algoritmo de Grover e implementación

El diagrama de bloques del algoritmo de Grover completo aparece representado en la siguiente figura:

Este algoritmo se estudiará en detalle en la última práctica de la asignatura, y su implementación se deja como trabajo al estudiante. La principal dificultad para aplicar el algoritmo de Grover en una palicación real es determinar un oráculo adecuado. En la práctica se considera el ejemplo de la implementación de una búsqueda en una base de datos muy sencilla.

13.3 Algoritmo de factorización de Shor

Dentro de los algoritmos cuánticos descubiertos hasta ahora, es especialmente relevante el algoritmo de Shor, que permite descomponer un número en sus factores primos. Este algoritmo tiene importantes implicaciones en la seguridad de Internet, ya que uno de los sistemas criptográficos de clave público-privada más empleados en la actualidad es el RSA que se basa precisamente en la dificultad computacional de factorizar un número grande en sus factores primos.

En esta sección estudiaremos las claves principales del algoritmo de factorización de Shor.

Transformada cuántica de Fourier

Uno los conceptos básicos de procesado de señal es el análisis de Fourier, que permite descomponer una señal en sus componentes frecuenciales. La transformada discreta de Fourier (DFT) para secuencias en tiempo discreto se define como $$\begin{align*} y_k = \frac{1}{\sqrt{N}} \sum_{\ell =0}^{N-1} e^{2\pi j\frac{k \ell}{N}} x_\ell, \quad k = 0,\ldots,N-1, \end{align*}$$ donde $x_\ell$, $\ell = 0,\ldots,N-1$, es una secuencia en tiempo discreto de longitud finita.

Esta operación transforma la secuencia $x_{\ell}$ al dominio frecuencial, $y_k$, $k = 0,\ldots,N-1$. Si consideramos las secuencias $x_\ell$ y $y_k$ como vectores $\boldsymbol{x}$ y $\boldsymbol{y}$, esta operación se puede reescribir como $$\begin{align*} \boldsymbol{y} = F \boldsymbol{x}, \end{align*}$$ donde $F$ se corresponde a una matriz unitaria.

En este curso hemos visto que los sistemas cuánticos admiten transformaciones unitarias, por lo que podríamos plantearnos la creación de un operador cuántico $F$ que calcula la transformada de Fourier de un estado cuántico. Esto es posible y es lo que se conoce como (QFT): $$\begin{align*} F \ket{k} = \frac{1}{\sqrt{N}} \sum_{\ell =0}^{N-1} e^{2\pi j\frac{k \ell}{N}} \ket{\ell}, \quad k = 0,\ldots,N-1 \end{align*}$$ donde $\ket{k}$ es el elemento $k$-ésimo de la base computacional. Este estado se define para un sistema cuántico de dimensión $n$ cúbits, de forma que la correspondiente base computacional tiene $N=2^n$ elementos.

Cálculo del periodo de una función

La transformada discreta de Fourier (DFT) se puede utilizar para encontrar el periodo de una función, ya que $$\begin{align*} x_\ell = x_{\ell + kL} \quad \Rightarrow \quad y_k = \text{DFT}\{x_\ell\} = 0, \ k \neq m N/L. \end{align*}$$ Así, la DFT de una función periódica se corresponde a una señal formada por deltas situadas en los múltiplos de la frecuencia fundamental.

Ejemplo 13.6 La siguiente figura muestra una secuencia $x_{\ell}$ periódica de longitud $N=20$ y periodo $L=4$, así como su correspondiente DFT $y_k$.

Se puede ver como la trasformada $y_k$ es una secuencia compuesta por deltas situadas en la frecuencia fundamental $N/L=5$ y sus múltiplos.

Del mismo modo, si aplicamos la transformada cuántica de Fourier (QFT) a un estado $\ket{\boldsymbol{x}}$ que presente un cierto periodo con respecto a la base computacional, entonces a su salida obtendremos un estado cuántico en el que no hay amplitud fuera de los múltiplos de la frecuencia fundamental. Así, si medimos el estado cuántico a la salida de la QFT obtendremos la frecuencia fundamental (o uno de sus armónicos).

Algoritmo de factorización

En 1992, Peter W. Shor propuso un algoritmo cuántico para la factorización de números utilizando que la QFT permite obtener el periodo de una función de una forma eficiente (Shor 1994). El algoritmo resultante presentaba una complejidad polinómica con el número de dígitos del número a factorizar, a diferencia del mejor algoritmo clásico para esta tarea, que presenta una complejidad exponencial (ver Ejercicio 9 de la Colección 4).

Planteamiento del problema: Consideremos un número entero $M$ tal que $M = A B$ con $A$ y $B$ primos. Asumimos que $M$ se puede representar con $n$ dígitos binarios, es decir $M < N = 2^n$. Para un $M$ dado, nos piden encontrar $A$ y $B$.

Algoritmo:

1. Elegir un número $a$ entre $1$ y $M-1$.
2. Si $\text{mcd}(a,M)\neq 1$, devolver $\text{mcd}(a,M)$.
3. Encontrar el periodo $L$ de la función $f(\ell) = a^{\ell} \text{ mod } M$

$\rightarrow$ si $L$ es par y $\text{mcd}(a^{L/2}+1, M)\neq M$, devolver $\text{mcd}(a^{L/2}+1, M)$

$\rightarrow$ en otro caso, devolver error

Este algoritmo se puede ejecutar en un ordenador clásico y permite obtener (con alta probabilidad) los factores de $M$. La ventaja de utilizar un ordenador cuántico viene a la hora de determinar el periodo $L$ de la función $f(\ell) = a^{\ell} \text{ mod } M$. Esta operación se puede realizar utilizando la QFT mediante un número de puertas cuánticas que crece polinomialmente con la longitud $n$ del número a factorizar. Por tanto, la única parte cuántica del algoritmo e correpondería a este proceso. A continuación aparece representado el diagrama de bloques correspondiente:

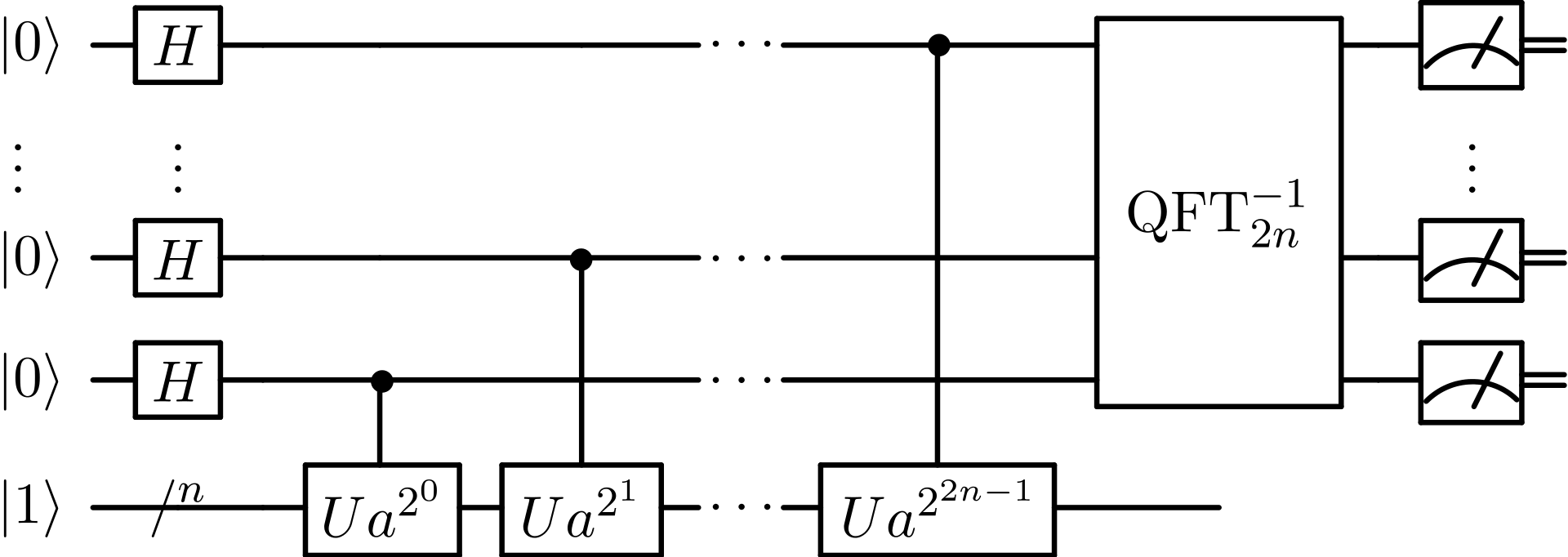
Si $n$ es el número de dígitos binarios, esta implementación cuántica requiere del orden de $\mathcal{O}\bigl(n^4\bigr)$ operaciones. Por otra parte, este es una algoritmo que ofrece no ofrece la solución de forma determinista, sino con alta probabilidad, por lo que es necesario repetir el algoritmo $\mathcal{O}(\log n)$ veces para conseguir factorizar el número con éxito. Así el algoritmo de factorización de Shor presenta una complejidad $\mathcal{O}\bigl(n^4\log n\bigr)$, que se puede comparar con la complejidad de uno de los mejores algoritmos de factorización clásicos como puede ser el algoritmo de Pollard y Strassen de 1976, que tiene complejidad $\mathcal{O}\bigl(2^{n/4} n^2 \bigr)$.

Ejemplo 13.7 Consideremos el problema de factorizar un número con $n=1024$ dígitos binarios.

• El algoritmo cuántico de Shor presentaría una complejidad del orden de $n^4\log n \approx 7,6 \cdot 10^{12}$.
• El algoritmo clásico de Pollard y Strassen requiere del orden de $2^{n/4} n^2 \approx 1,2 \cdot 10^{83}$ operaciones.

Para tener algo de intuición sobre la diferencia de magnitud de estas cantidades, asumamos que el tiempo para realizar una operación fuera similar en ambas implementaciones. Entonces, si el algoritmo de Shor tarda $1$ segundo en realizar la factorización, el algoritmo de Pollard y Strassen tardaría en torno a $5 \cdot 10^{62}$ años en realizar la misma tarea.

Muchos de los sistemas criptográficos usados en la actualidad, como por ejemplo RSA, se basan en la dificultad de factorizar números grandes. Entonces, ¿están estos sistemas criptográficos amenazados? Para responder a esta pregunta, se debe tener en cuenta el estado de la tecnología de computación cuántica hoy.

Para implementar el algoritmo de Shor con un ordenador cuántico ideal, se necesitarían $2$ cúbits por cada dígito binario del número a factorizar (en la práctica, debido al ruido existente se necesitarían entre $2$ y $10$ cúbits por cada dígito binario a factorizar. La tecnología actual con ordenadores de $\sim 70$ cúbits, permitiría (en el mejor de los casos) factorizar números de hasta $35$ bits. Así, teniendo en cuenta que que las claves RSA actuales tienen una longitud de entre $1024$ y $2048$ bits, podemos concluir que este algoritmo (todavía) no presenta una amenaza a la seguridad de nuestras comunicaciones.

Referencias

Deutsch, David. 1985. “Quantum Theory, the Church–Turing Principle and the Universal Quantum Computer.” Proc. R. Soc. Lond. A 400: 97–117. https://doi.org/10.1098/rspa.1985.0070.

Deutsch, David, and Richard Jozsa. 1992. “Rapid Solution of Problems by Quantum Computation.” Proc. R. Soc. Lond. A 439: 553–58. https://doi.org/10.1098/rspa.1992.0167.

Grover, L. K. 1996. “A Fast Quantum Mechanical Algorithm for Database Search.” In Proceedings of 28th Annual ACM Symposium on the Theory of Computing, 212–19. Philadelphia, Penn. USA. https://doi.org/10.1145/237814.237866.

Shor, Peter W. 1994. “Algorithms for Quantum Computation: Discrete Logarithms and Factoring.” In Proceedings 35th Annual Symposium on Foundations of Computer Science, 124–34. https://doi.org/10.1109/SFCS.1994.365700.