8 Transmisión de información

Como hemos visto en los temas anteriores, la naturaleza de la mecánica cuántica implica que la evolución física de un estado es siempre de la forma: $$\begin{align*} \rho \ \rightarrow\ \sigma = U \rho U^H \end{align*}$$ donde $U$ es un operador unitario y, por tanto, $U^H = U^{-1}$ se corresponde con su inversa.

Denominamos canal cuántico a un proceso que realiza una transformación unitaria sobre un determinado estado cuántico. Posibles ejemplos serían la transmisión de un fotón por una fibra óptica o un cambio en el spin de un electrón en un circuito eléctrico. El hecho de que la transformación sea unitaria facilita en gran medida el diseño de un sistema de comunicaciones para la transmisión de información a través del canal considerado. Existen dos posibles escenarios estrechamente relacionados:

• Transmisión de información cuántica: El sistema de comunicaciones debe transmitir un estado o una secuencia de estados cuánticos, sin destruir la información que contienen.
• Transmisión de información clásica: En este caso el sistema de comunicaciones debe transmitir una secuencia binaria de unos y ceros, sin errores o minimizando la probabilidad de error en el receptor.

A pesar de que son dos problemas conceptualmente diferentes, veremos que es posible encapsular información clásica en un estado cuántico, y por tanto es posible la transmisión de información clásica a través de un canal cuántico.

8.1 Información cuántica

Consideremos un estado $\rho$ que se transmite sobre un canal cuántico $U$ con salida $\sigma= U \rho U^H$:

Dado que una transformación unitaria siempre es invertible, si conocemos la matriz $U$ es posible recuperar el estado original compensando la distorsión que introduce el canal. Para ello, aplicamos una transformación $U^H$ al estado cuántico recibido: $$\begin{align*} \hat\rho &= U^H \sigma U\\ &= U^H U \rho U^H U = \rho \end{align*}$$ ya que $U^H U = I$ se corresponde con la matriz identidad. De esta forma, si la transformación $U$ es conocida, es posible utilizar un canal cuántico para la transmisión de información cuántica, y recuperar perfectamente el estado cuántico transmitido.

Ejemplo 8.1 Queremos transmitir un estado cuántico binario $\rho = \ket{0}\bra{0} = \left[\begin{smallmatrix}1&0\\0&0\end{smallmatrix}\right]$ sobre un canal $$\begin{align*} U = \frac{1}{\sqrt{2}} \left[\begin{matrix}+1&+1\\+1&-1\end{matrix}\right],\quad U^H = U, \end{align*}$$ donde la matriz $U$ se asume conocida en el receptor. En este caso, la salida del canal está dada por $$\begin{align*} \sigma = U \rho U^{H} = \frac{1}{2} \left[\begin{matrix}1&1\\1&1\end{matrix}\right]. \end{align*}$$ Para recuperar el estado original, invertimos la transformación introducida por el canal $$\begin{align*} \hat\rho &= U^{H} \sigma U = \frac{1}{4} \left[\begin{matrix}1&1\\1&-1\end{matrix}\right] \left[\begin{matrix}1&1\\1&1\end{matrix}\right] \left[\begin{matrix}1&1\\1&-1\end{matrix}\right] = \left[\begin{matrix}1&0\\0&0\end{matrix}\right] = \rho. \end{align*}$$

Podemos ver que hemos recuperado el estado original. Esto ocurre no solo para el estado considerado en este ejercicio, sino para para cualquier estado $\rho$ a la entrada del canal. Entonces, con este esquema podemos transmitir sin errores un cúbit de información a través de este canal cuántico binario.

 Jupyter notebooks: Octave, Python

8.2 Información clásica

Es posible utilizar un canal cuántico para enviar información clásica. Para ello, se deben asignar los posibles valores a transmitir a una serie de estados a la entrada del canal (codificación), y definir un POVM para realizar una medida a la salida del canal (decodificación).

El diagrama de bloques de este sistema de comunicaciones para la transmisión de un bit de información clásica $m\in\{0,1\}$ aparece representado a continuación:

Vamos a considerar el caso un canal cuántico binario, es decir, la transformación $U$ se corresponde a una matriz unitaria de dimensión $2\times 2$. El sistema de comunicaciones aparece descrito a continuación:

• Codificador: En función del mensaje a transmitir $m\in\{0,1\}$, el transmisor prepara uno de los siguientes estados a la entrada del canal: $$\begin{align*} \rho = \begin{cases} \rho_0 = \ket{0}\bra{0},&m=0\\ \rho_1 = \ket{1}\bra{1},&m=1 \end{cases} \end{align*}$$

• Canal: A la salida del canal recibimos el estado $\sigma = U \rho U^{H}$. Así, en función del bit transmitido, $$\begin{align*} \sigma= \begin{cases} \sigma_0 = U \rho_0 U^{H},&m=0\\ \sigma_1 = U \rho_1 U^{H},&m=1 \end{cases} \end{align*}$$

• Decodificador: El decodificador aplica un proceso de medida al estado recibido $\sigma$ con respecto al POVM $\{\tilde\Pi_{0}, \tilde\Pi_{1}\}$, donde $$\begin{align*} \tilde\Pi_{0} &= U \Pi_{0} U^{H},\\ \tilde\Pi_{1} &= U \Pi_{1} U^{H}, \end{align*}$$ con $\Pi_0 = \ket{0}\bra{0}$ y $\Pi_1 = \ket{1}\bra{1}$. El resultado de este proceso de medida será una estimación $\hat{m}$ del mensaje transmitido.

Probabilidad de error

Definimos la probabilidad de error del sistema como la probabilidad de que para un mensaje transmitido $m\in\{0,1\}$, el mensaje decodificado sea $\hat{m} \neq m$.

En nuestro sistema existen dos eventos de error: si el símbolo transmitido es $m=0$ y decodificamos $\hat{m}=1$, o si transmitimos $m=1$ y decodificamos $\hat{m}=1$. Así, escribimos la probabilidad de error del sistema como $$\begin{align*} P_{\text{e}} &= \Pr\{ M \neq\hat{M} \}\\ &= \Pr\{ M=0, \hat{M}=1 \} + \Pr\{ M=1, \hat{M}=0 \}\\ &= \Pr\{ M=0 \} \Pr\{ \hat{M}=1 \;|\; M=0 \} + \Pr\{ M=1 \} \Pr\{ \hat{M}=0 \;|\; M=1 \}, \end{align*}$$ donde en el último paso hemos aplicado la regla de la cadena.

Para el sistema de comunicaciones descrito se tiene que $$\begin{align*} \Pr\{ \hat{M}=1 \;|\; M=0 \} = \text{Tr}\bigl[\tilde\Pi_{1} \sigma_0\bigr] = \text{Tr}\bigl[U \Pi_{1} U^{H} U \rho_{0} U^{H}\bigr] = \text{Tr}\bigl[\Pi_{1} \rho_{0}\bigr] = 0,\\ \Pr\{ \hat{M}=0 \;|\; M=1 \} = \text{Tr}\bigl[\tilde\Pi_{0} \sigma_1\bigr] = \text{Tr}\bigl[U \Pi_{0} U^{H} U \rho_{1} U^{H}\bigr] = \text{Tr}\bigl[\Pi_{0} \rho_{1}\bigr] = 0, \end{align*}$$ dado que $U^{H} U = U U^{H} = \boldsymbol{I}$ y donde hemos usado que los proyectores $\Pi_i$ y los estados $\rho_j$ son ortogonales entre sí para $i\neq j$. Por tanto, concluimos que la probabilidad de error está dada por $$\begin{align*} P_{\text{e}} &= \Pr\{ M \neq\hat{M} \}\\ &= \Pr\{ M=0 \} 0 + \Pr\{ M=1 \} 0 = 0, \end{align*}$$ independientemente de las probabilidades del mensaje de entrada $\Pr\{ M=m \}$.

Concluimos que este sistema de comunicaciones permite la transmisión sin errores de un bit clásico sobre un canal cuántico binario. Esto ocurre porque hemos escogido unas palabras código o estados código $\rho_0$ y $\rho_1$ que son ortogonales entre sí, es decir, tales que $\text{Tr}[\rho_0\rho_1] = 0$.

En un espacio de dimensión 2, no es posible definir 3 (o más) operadores ortogonales entre sí, por lo que no será posible transmitir sin errores más de un bit clásico de información sobre un único uso de un canal cuántico binario.

Ejemplo 8.2 Considere el canal definido por $$\begin{align*} \text{U} = \left[\begin{smallmatrix}0 &1\\1&0\end{smallmatrix}\right], \end{align*}$$ y el esquema descrito anterioremente para la transmisión de un bit $m=0$:

1. El codificador genera un estado a la entrada del canal $$\begin{align*} \rho = \ket{0}\bra{0} = \left[\begin{smallmatrix}1 &0\\0&0\end{smallmatrix}\right]. \end{align*}$$
2. A la salida del canal recibimos el estado $$\begin{align*} \sigma = U\rho U^H = \left[\begin{smallmatrix}0 &1\\1&0\end{smallmatrix}\right] \left[\begin{smallmatrix}1 &0\\0&0\end{smallmatrix}\right] \left[\begin{smallmatrix}0 &1\\1&0\end{smallmatrix}\right] = \left[\begin{smallmatrix}0 &0\\0&1\end{smallmatrix}\right]. \end{align*}$$
3. La medida de este estado se realiza con respecto al POVM $\{\tilde\Pi_{0}, \tilde\Pi_{1}\}$, donde $$\begin{align*} \tilde\Pi_{0} = U \Pi_{0} U^{H} = \left[\begin{smallmatrix}0 &0\\0&1\end{smallmatrix}\right],\qquad \tilde\Pi_{1} = U \Pi_{1} U^{H} = \left[\begin{smallmatrix}1 &0\\0&0\end{smallmatrix}\right]. \end{align*}$$ Así las probabilidades de observar $\hat{m}=0$ y $\hat{m}=1$ están dadas por $$\begin{align*} \Pr\{ \hat{M}=0 \;|\; M=0 \} &= \text{Tr}\bigl[\tilde\Pi_{0} \sigma_0\bigr] = \text{Tr}\Bigl[\left[\begin{smallmatrix}0 &0\\0&1\end{smallmatrix}\right] \left[\begin{smallmatrix}0 &0\\0&1\end{smallmatrix}\right]\Bigr] = 1,\\ \Pr\{ \hat{M}=1 \;|\; M=0 \} &= \text{Tr}\bigl[\tilde\Pi_{1} \sigma_0\bigr] = \text{Tr}\Bigl[\left[\begin{smallmatrix}1 &0\\0&0\end{smallmatrix}\right] \left[\begin{smallmatrix}0 &0\\0&1\end{smallmatrix}\right]\Bigr] = 0. \end{align*}$$

Concluimos que siempre se observa el estado correcto, $\hat{m}=0$ con probabilidad $1$. De forma análoga se puede analizar la transmisión de un bit $m=1$, observando $\hat{m}=1$ en este caso.

 Jupyter notebooks: Octave, Python

8.3 Transmisión por entrelazamiento

En las secciones anteriores hemos estudiado el problema de transmisión de información a través de un canal cuántico. Ahora nos vamos a plantear la pregunta de si es posible transmitir 1 bit de información clásica utilizando un estado entrelazado compartido entre el transmisor y el receptor. Para presentar el esquema planteado, denominaremos al transmisor Alice y al receptor Bob. La idea de la transmisión de información por entrelazamiento aparece representada en la siguiente figura:

Los pasos necesarios para transmitir un bit entre Alice y Bob estarían dados por el siguiente protocolo:

1. Se genera un estado cuántico máximamente entrelazado (ebit). Cada uno de los dos cúbits que lo componen se distribuyen a Alice y a Bob, por lo que estos pasan a compartir el estado entrelazado.
2. Alice define dos conjuntos de proyectores diferentes para realizar una medida, POVM$_0$ y POVM$_1$. En función del bit $m\in\{0,1\}$ a transmitir, Alice realiza una operación de medida con el POVM$_m$.
3. El proceso de medida de Alice colapsa el estado entrelazado completo, por lo que también afecta a la parte del ebit de la que dispone el receptor Bob.
4. Bob mide su parte del ebit para intentar discriminar qué POVM ha aplicado Alice a partir del resultado de esta medida, y así determinar el bit transmitido $m$.

Se debe tener en cuenta que la distribución del ebit está limitada por la velocidad de la luz: un estado entrelazado surge de un proceso físico conjunto y no se puede generar de forma separada. Por la teoría de la relatividad general, no es posible transportar un fotón u otro estado cuántico más rápido que la velocidad de la luz. Sin embargo, el colapso de la función de onda es instantáneo, independientemente de la distancia que separe a Alice y a Bob, por lo que una medida en el laboratorio de Alice (transmisor) se reflejaría de forma instantánea en el laboratorio de Bob (receptor). Así, en caso de funcionar, ¡el esquema descrito implicaría la transmisión de información más rápido que la velocidad de la luz!

Esta observación nos debería hacer sospechar que este sistema de comunicaciones no es posible, ya que no cumple la teoría de la relatividad general propuesta por Einstein. El siguiente ejemplo, aunque no sea una demostración rigurosa, muestra por qué Bob no puede determinar qué POVM ha aplicado Alice, y, por tanto, por qué este sistema de comunicaciones no se puede implementar en la práctica:

Ejemplo 8.3 Definimos el estado máximamente entrelazado $$\begin{align*} \delta^{AB} = \frac{1}{2} \left[\begin{smallmatrix} 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 1 \end{smallmatrix}\right] \end{align*}$$ donde el superíndice $AB$ hace referencia a que la primera parte del estado pertenece a Alice y la segunda a Bob. Consideramos los proyectores de medida: $$\begin{align*} \Pi_{0}^A=\begin{bmatrix}1&0\\0&0\end{bmatrix},\quad \Pi_{1}^A=\begin{bmatrix}0&0\\0&1\end{bmatrix},\quad \Pi_{+}^A=\frac{1}{2}\begin{bmatrix}+1&+1\\+1&+1\end{bmatrix},\quad \Pi_{-}^A=\frac{1}{2}\begin{bmatrix}+1&-1\\-1&+1\end{bmatrix}. \end{align*}$$ Ahora, Alice aplica una medida a su parte del estado compartido con Bob:

• Si $m=0$, Alice aplica la medida con respecto al POVM$_{01} = \bigl\{\Pi^A_{0},\Pi^A_{1}\bigr\}$.
• Si $m=1$, Alice aplica la medida con respecto al POVM$_{+-} =\bigl\{\Pi^A_{+},\Pi^A_{-}\bigr\}$.

Para aplicar la medida al estado conjunto, definimos las matrices de dimensión $4\times 4$ dadas por $\Pi_k^{AB} = \Pi_k^A \otimes \boldsymbol{I}_2^B$, donde $k\in\{0,1,+,-\}$. Así, si Alice aplica el POVM$_{01}= \bigl\{\Pi_{0}^A,\Pi_{1}^A\bigr\}$, y teniendo en cuenta que Bob no puede conocer el resultado de la medida, obtenemos el nuevo estado conjunto: $$\begin{align*} \theta_{01}^{AB} = \Pi_{0}^{AB} \delta^{AB} \Pi_{0}^{AB} + \Pi_{1}^{AB} \delta^{AB} \Pi_{1}^{AB} = \frac{1}{2} \left[\begin{smallmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{smallmatrix}\right]. \end{align*}$$

Si Alice aplica el POVM$_{+-} =\bigl\{\Pi_{+}^A,\Pi_{-}^A\bigr\}$, como Bob no conoce el resultado de la medida, obtenemos: $$\begin{align*} \theta_{+-}^{AB} = \Pi_{+}^{AB} \delta^{AB} \Pi_{+}^{AB} + \Pi_{-}^{AB} \delta^{AB} \Pi_{-}^{AB} = \frac{1}{4} \left[\begin{smallmatrix} 1 & 0 & 0 & 1\\ 0 & 1 & 1 & 0\\ 0 & 1 & 1 & 0\\ 1 & 0 & 0 & 1 \end{smallmatrix}\right]. \end{align*}$$ El estado conjunto tras aplicar la medida es diferente en los dos casos, $\theta_{01}^{AB} \neq \theta_{+-}^{AB}$.

Sin embargo, Bob no tiene acceso a este estado conjunto, sino solo a una parte del mismo. Para conocer el estado desde el punto de vista de Bob, debemos marginalizar $\theta^{AB}$ eliminando la parte de Alice. Se tiene que $$\begin{align*} \sigma^B_{01} = \text{Tr}_A\bigl[\theta_{01}^{AB}\bigr] = \frac{1}{2} \left[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\right],\qquad \sigma^B_{+-} = \text{Tr}_A\bigl[\theta_{+-}^{AB}\bigr] = \frac{1}{2} \left[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\right]. \end{align*}$$ Podemos ver que $\sigma^B_{01} = \sigma^B_{+-}$. Así, Bob no puede distinguir ambos casos teniendo aceso únicamente a su parte del estado. Por tanto, la comunicación no es posible con este esquema.

 Jupyter notebooks: Octave, Python

Con este ejemplo podemos ver la clave que imposibilita la transmisión de información en este sistema. Independientemente de las bases de medida que Alice elija para medir su parte del estado, si Bob no tiene acceso al resultado de esa medida, su parte del estado entrelazado se transforma siempre en el estado máximamente mezclado $\sigma^B = \frac{1}{2} \left[\begin{smallmatrix} 1 & 0 \\ 0 & 1 \end{smallmatrix}\right]$, y por tanto su medida no aportaría información sobre el proceso realizado en Alice.

A pesar de que el sistema propuesto en este ejemplo no funciona, desde el punto de vista físico no es evidente que no se puedan establecer comunicaciones a través del entrelazamiento utilizando un protocolo más sofisticado. De hecho, en 1982 el físico experimental Nick Herbert propuso un esquema de transmisión de información utilizando este principio que acabaría publicado en una revista científica. El montaje experimental propuesto por Herbert se muestra en la siguiente figura, tomada del artículo “Transmisor superlumínico basado en un nuevo tipo de medida cuántica” (Herbert 1982):

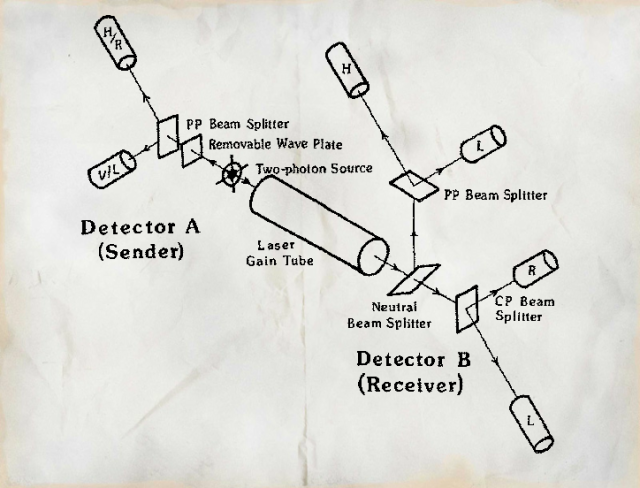
La única diferencia entre este sistema y el analizado en el Ejemplo 8.3 es el cilindro etiquetado como Laser Gain Tube que, a partir de un fotón, puede producir múltiples fotones idénticos al primero. En este bloque se generarían así varias copias de la parte de Bob del estado $\delta^{AB}$, lo que sí le permitiría distinguir entre las dos posibles medidas de Alice para $m=0$ y $m=1$. Así, podríamos comunicarnos a velocidades más rápidas que la luz… ¿o no? La publicación de este “transmisor superlumínico” muestra como avanza el progreso científico moderno. Tal y como es habitual, el artículo de Herbert fue revisado por otros investigadores de su área antes de su publicación. Uno de estos revisores escribiría años más tarde (Peres 2003):

Recomendé al editor de Foundations of Physics que se publique este artículo. Escribí que era obviamente incorrecto, pero esperaba que generara un considerable interés y que encontrar el error condujera a un progreso significativo en nuestra comprensión de la física.

El revisor tenía razón y en los siguientes meses se produjo un gran revuelo en el área que llevó a una serie de avances en la comprensión de la mecánica cuántica. Fruto de este trabajo fue el descubrimiento del teorema de la no clonación, que impide crear copias de un estado cuántico (Wootters and Zurek 1982) (Dieks 1982).

Teorema 8.1 (Teorema de la no clonación) De acuerdo a los principios de la mecánica cuántica, no existe una operación de clonación $f: \mathcal{H} \to \mathcal{H}^{\otimes 2}$, tal que, para cada $\rho$, se cumpla que $f(\rho) = \rho^{\otimes2}$.

Demostración. La evolución de un sistema cuántico es unitaria. Asumamos que existe un operador unitario $U$ de clonación que actúa sobre un estado puro $\ket{\psi}$ y un estado auxiliar $\ket{a}$ independiente de $\ket{\psi}$, de forma que a su salida obtenemos dos copias de su entrada: $$\begin{align*} U \bigl( \ket{\psi} \otimes \ket{a} \bigr) = \ket{\psi} \otimes \ket{\psi}. \end{align*}$$ El estado auxiliar $\ket{a}$ es necesario para que la dimensión de la salida coincida con la dimensión de la entrada, tal y como requiere un operador unitario. Si existe esta operación de clonación, también debe funcionar para los estados de la base $\ket{0}$ y $\ket{1}$. Así, se debe cumplir que $$\begin{align} U \bigl( \ket{0} \otimes \ket{a} \bigr) = \ket{0} \otimes \ket{0} = \ket{00}, \tag{1}\\ U \bigl( \ket{1} \otimes \ket{a} \bigr) = \ket{1} \otimes \ket{1} = \ket{11}. \tag{2} \end{align}$$ Para un estado arbitrario $\ket{\psi}$ dado por la superposición $\ket{\psi} = \alpha \ket{0} + \beta \ket{1}$, se tiene que $$\begin{align*} \ket{\psi} \otimes \ket{a} &= \bigl(\alpha \ket{0} + \beta \ket{1}\bigr) \otimes \ket{a}\\ &= \alpha \bigl(\ket{0}\otimes \ket{a}\bigr) + \beta \bigl(\ket{1}\otimes \ket{a}\bigr). \end{align*}$$ Utilizando la linealidad del operador $U$ junto con $(1)$-$(2)$, obtenemos $$\begin{align} U \bigl(\ket{\psi} \otimes \ket{a}\bigr) &= \alpha U \bigl(\ket{0}\otimes \ket{a}\bigr) + \beta U \bigl(\ket{1}\otimes \ket{a}\bigr) \notag\\ &= \alpha \ket{00} + \beta \ket{11}. \tag{3} \end{align}$$ Sin embargo, dada la propiedad distributiva del producto de Kronecker, se cumple $$\begin{align} \ket{\psi} \otimes \ket{\psi} &= \bigl(a \ket{0} + \beta \ket{1}\bigr) \otimes \bigl(\alpha \ket{0} + \beta \ket{1}\bigr) \notag\\ &= \alpha^2 \ket{00} + \alpha\beta \ket{01} + \beta\alpha \ket{10} + \beta^2 \ket{11}. \tag{4} \end{align}$$ Comparando $(3)$-$(4)$, concluimos que $$\begin{align*} U \bigl(\ket{\psi} \otimes \ket{a}\bigr) \neq \ket{\psi} \otimes \ket{\psi}, \end{align*}$$ y, por tanto, no existe un operador unitario $U$ que clone un estado arbitrario.

Así, no es posible que el tubo de ganancia láser (Laser Gain Tube) genere copias perfectas de un fotón dado e imposibilita la transmisión de información a velocidades superlumínicas. La propiedad de la no clonación resultará también fundamental otro área de las comunicaciones cuánticas que estudiaremos en la Sección 10: Criptografía cuántica.

8.4 Sistemas ruidosos

Hasta ahora hemos asumido que los canales cuánticos son ideales y que se modelan con una transformación unitaria. En este caso, para poder reconstruir el estado original a partir de la salida del canal necesitamos:

1. Tener acceso al estado cúantico de salida $\sigma$.
2. Conocer la transformación $U$ aplicada por el canal.

Ambos puntos son importantes y no siempre se cumplen. Por ejemplo, en un sistema que interacciona con el entorno, es posible que no tengamos acceso a una parte del estado de salida (sistema abierto), o que no conozcamos exactamente la transformación que ha introducido el canal. Esto aparece ilustrado en la siguiente figura, que muestra un sistema abierto en el que $\rho$ y $\sigma$ son las señales de interés, mientras que $\rho_E$ y $\sigma_E$ representan el estado cuántico del entorno, sobre el que no tenemos control ni acceso a su estado.

En los sistemas abiertos, tal y como el mostrado en la figura anterior, el canal entre $\rho$ y $\sigma$ ya no se puede modelar como una transformación unitaria. En estos casos, se puede decir que el canal “introduce errores” y produce una transformación no reversible. Algunos ejemplos de este tipo de canales son:

• Canal cuántico binario bit-flip: $$\begin{align*} \sigma = (1-\epsilon) \; \rho + \epsilon \; X \rho X \quad \text{ donde } \quad X = \bigl[\begin{smallmatrix}0&1\\1&0\end{smallmatrix}\bigr] \end{align*}$$

• Canal cuántico binario de borrado: Dado un estado de borrado $\ket{e}$ (ortogonal a $\ket{0}$ y $\ket{1}$), $$\begin{align*} \sigma = (1-\epsilon) \rho + \epsilon \ket{a}\bra{e} \end{align*}$$

• Canal cuántico binario de eliminación de fase: $$\begin{align*} \sigma = (1-\epsilon) \; \rho + \epsilon \; Z \rho Z \quad \text{ donde } \quad Z = \bigl[\begin{smallmatrix}1&0\\0&-1\end{smallmatrix}\bigr] \end{align*}$$

Ejercicio 8.1 Considere un canal cuántico bit flip, descrito por la siguiente ecuación $$\begin{align*} \sigma = (1-\epsilon) \rho + \epsilon X \rho X\quad \text{donde}\quad X = \bigl[\begin{smallmatrix} 0&1\\1&0 \end{smallmatrix}\bigr]. \end{align*}$$

• Demuestre que $X \rho X$ es una operación reversible para cualquier valor de $\rho$.
• A pesar de que $X \rho X$ es reversible, si $0<\epsilon<1$, la transformación producida por el canal no lo es. ¿Se trata de una evolución de un sistema cerrado o una evolución en un sistema abierto?
• Para $\epsilon = 1/2$, obtenga la salida del canal cuando $\rho = \ket{0}\bra{0}$. Repita este apartado cuando $\rho = \ket{1}\bra{1}$. ¿Qué puede concluir sobre la probabilidad de error de un sistema de comunicaciones sobre este canal que codifique el bit $0$ como $\rho_0 = \ket{0}\bra{0}$ y el bit $1$ como $\rho_1 = \ket{1}\bra{1}$?

 Jupyter notebooks: Octave, Python

En este curso no entraremos en detalles sobre como conseguir una comunicación fiable en sistemas ruidosos, problema que se enmarca en el ámbito de la teoría de la información cuántica. Al igual que en el caso clásico, es necesario un código que introduzca redundancia sobre sucesivos usos del canal pero, a diferencia del caso clásico, para obtener prestaciones óptimas es necesario realizar una medida conjunta sobre las salidas de esos sucesivos usos del canal.

En su lugar, en las siguientes secciones asumiremos un canal cuántico ideal (sin errores), y estudiaremos varios esquemas de transmisión que utilizan las leyes de la mecánica cuántica de una forma no trivial, y que resultan en sistemas de comunicaciones que no tienen un equivalente clásico. De esta forma nos centraremos en las nuevas aplicaciones y el cambio de paradigma que implican las comunicaciones cuánticas.

Referencias

Dieks, D. 1982. “Communication by EPR Devices.” Physics Letters A 92: 271–72. https://doi.org/10.1016/0375-9601(82)90084-6.

Herbert, Nick. 1982. “FLASH—a Superluminal Communicator Based Upon a New Kind of Quantum Measurement.” Foundations of Physics 12 (December): 1171–79. https://doi.org/10.1007/BF00729622.

Peres, A. 2003. “How the No-Cloning Theorem Got Its Name.” Fortschritte Der Physik 51: 458–61. https://doi.org/10.1002/prop.200310062.

Wootters, William K., and Wojciech H. Zurek. 1982. “A Single Quantum Cannot Be Cloned.” Nature 299 (October): 802–3. https://doi.org/10.1038/299802a0.